11. Linear programming

At the seminar, we showed how to use linear programming to approximate the solution of some computationally hard problem. In the homework, we will connect linear programming with another topic we have covered during the semester, namely geometry. The problem statement is as follows.

Given a convex polygon $M$ with $n$ sides such that none of its sides is vertical. Let $i$-th side of the polygon $M$ lie on the line $\ell_i$ given by the equation $y = a_ix + b_i$, where $i\in\{1,2,\ldots,n\}$. Find a circle with centre $\mathbf{s}=(s_1,s_2)$ and radius $r$ such that it is entirely contained in $M$ and its radius is maximal.

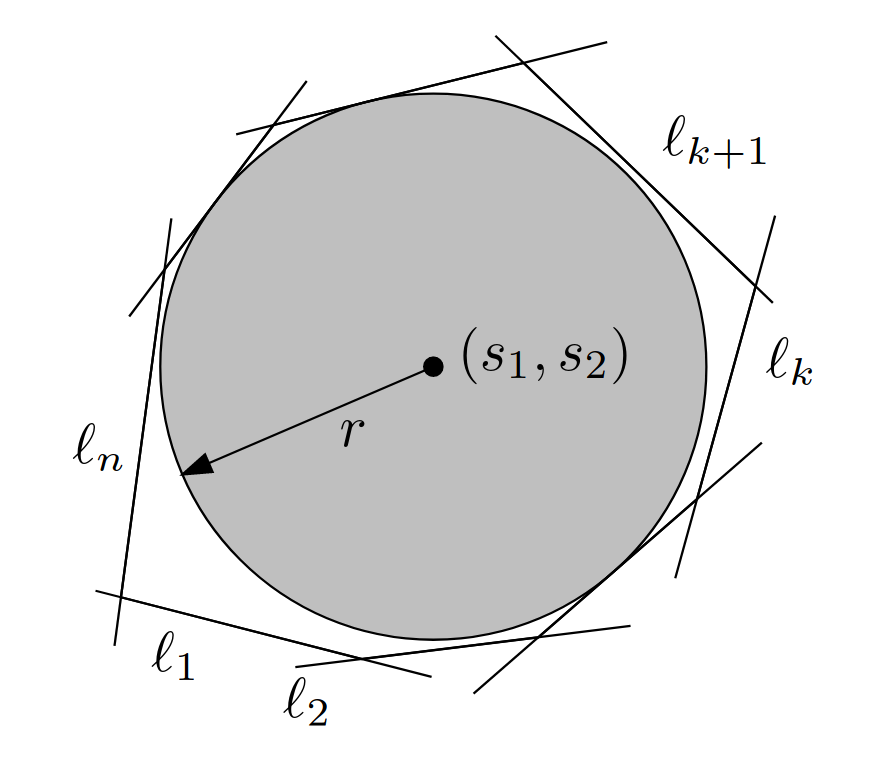
Your solution must contain the deduction, justification and general formulation of a linear programme solving the given problem. Next, prepare some example of such a polygon $M$ with at least $n \geq 7$ sides and formulate this problem for the solver used throughout the lecture. Let the solution code be part of your submission.