2. Domácí úkol: Fermi-Ulam

Úvod

Na začátku první poloviny dvacátého století se zjistilo, že do Zemské atmosféry dopadají vysokoenergetické částice tzv. "vesmírného záření" (Nobelova cena za fyziku pro Victora Hesse z roku 1936). Toto záření má velmi praktický vliv například na životnost elektronických zařízení ve vesmíru a nepřestává být objektem výzkumu ani v současnosti. Zdroje tohoto záření jsou různorodé (Slunce, výbuchy supernov, teorií je mnoho). Dnes víme, že energie částic tohoto záření může být až $3\cdot10^{20}\,\mathrm{eV}$ , tedy asi $40\cdot10^6$ větší, než jaké jsme uměle schopni dosáhnout v největším dnešním urychlovači (Large Hadron Collider v CERNu).

Otázka původu tohoto záření zajímala řadu vědců. Enrico Fermi vyslovil [1] teorii, že tyto částice jsou na své vysoké energie urychlovány měnícími se magnetickými poli v mezigalaktickém prostoru. Polský matematik Stanislaw Ulam v roce 1961 vytvořil [2] mechanický model, který se snažil tento proces popsat a prozkoumat.

V tomto cvičení budeme implementovat přesně tento mechanický model a experimentálně se podíváme na jeho chování.

Teoretický background

Popis modelu

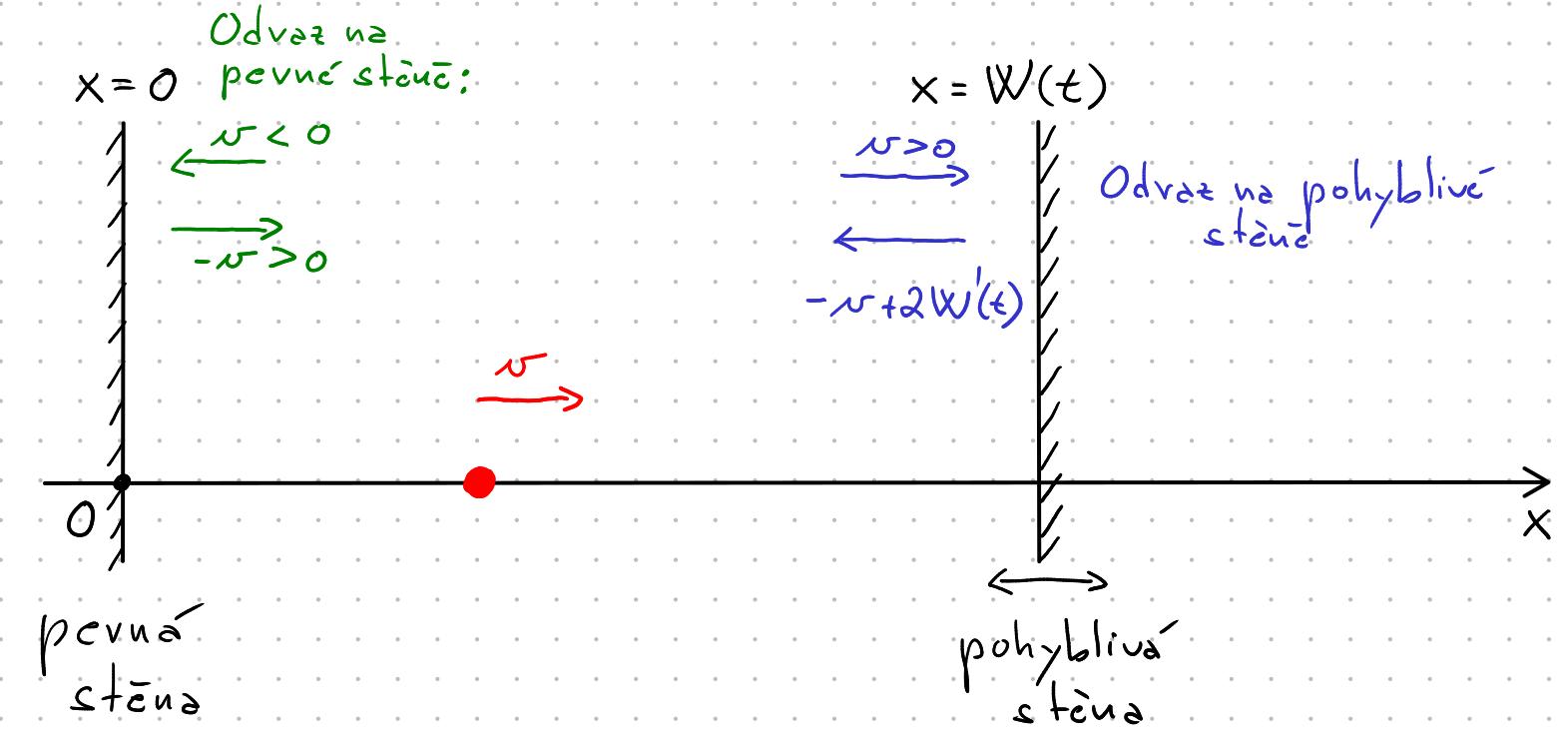
Představme si kuličku (hmotný bod), která se pohybuje mezi dvěma zdmi po ose $x$ z nichž jedna je pevná (dejme tomu ta vlevo, stojící v bodě $x=0$ ) a druhá periodicky osciluje, její poloha je v závislosti na čase popsána periodickou spojitou funkcí $x = W(t)$ s periodou $T > 0$ . Přirozeně předpokládáme platnost nerovnosti $W(t) > 0$ pro všechna $t \in \mathbb{R}$ , tj. zdi do sebe nenarážejí. Na těchto zdech se kulička odráží dokonale (bez tlumení), podrobněji odraz popíšeme v následujícím odstavci.

Z pevné zdi vypustíme kuličku v čase $t_0 = 0$ ve směru pohyblivé zdi s rychlostí $v_0 > 0$ . Kulička narazí do pohyblivé zdi v čase $t_c$ a odrazí se s rychlostí $v_c := -v_0 + 2W'(t_c)$ (proč? představte si celou situaci ve vztažném systému pohyblivé zdi, tj. jako byste na pohyblivé zdi seděli). Poté cestuje zpět k nepohyblivé zdi rychlostí $v_c < 0$ , ke které dorazí v čase $t_1$ . Od té se zase odrazí zpět s rychlostí $v_1 := -v_c$ a letí směrem k pohyblivé zdi, atd.

Pozor! Při malých rychlostech, resp. divoce oscilujících zdech, může dojít k vícenásobným odrazům na pohyblivé zdi. Pro zjednodušení úlohy se k této situaci budeme stavět následovně:

pokud po první nalezeném odrazu na pohyblivé zdi má kulička už zápornou rychlost, tak možnost druhého odrazu (zeď se rychle vrátí) ignorujeme. Rovnou počítáme s návratem kuličky. Toto není velké omezení, protože nám jde o větší rychlosti kuličky, kde k této situaci nebude docházet.
pokud po první kolizi kuličky s pohyblivou zdí kulička ještě neletí zpět (tato situace skutečně může nastat a nastane opět pro pomalu se pohybující kuličku), tak uměle změníme směr rychlosti (z $v > 0$ na $-v < 0$ ).

K popisu modelu. — Obrázek 2. Grafické znázornění modelu.

Hledání času kolize

K hledání kolize můžete použít (ale nemusíte, kreativně nejste svázáni) metodu sečny.

Metoda sečny je analog Newtonovy metody, která je použitelná i pro funkce nemající v některých bodech derivaci (takové oscilace zdi nás také budou zajímat, protože dávají zajímavé výsledky). Její myšlenka je jednoduchá: chceme najít nulový bod funkce $f$ a k dispozici máme dvě aproximace, odhady, tohoto bodu $x_1$ a $x_2$ . Není podstatné, jestli očekávaný nulový bod leží mezi těmito body nebo ne. Tuto aproximaci vylepšíme (doufáme) podobně jako v Newtonově metodě, jen místo tečny použijeme sečnu (pro jejíž výpočet není potřeba derivace):

Sestrojme odpovídající sečnu grafu funkce $f$ , tj. přímku procházející body $(x_1, f(x_1))$ a $(x_2, f(x_2))$ a najděme průsečík této sečny s osou $x$ , který označíme $x_3$ .
Celý proces nyní opakujeme s $x_2$ a $x_3$ a tak dále, dokud platí $|x_{n+1} - x_n| > \varepsilon$ , kde $\varepsilon$ je zadaná přesnost, nebo dokud nedosáhneme maximálního počtu iterací. V prvním případě vracíme jako výsledek poslední vypočtenou aproximaci, tj. $x_{n+1}$ . V druhém případě vyvoláme výjimku, požadované přibližné řešení jsme nenalezli.

Vizualizace

Jak vývoj naší kuličky popsat? Mohli bychom jistě vytvořit animaci, jak se kulička odráží od zdí. To ale nebude příliš vypovídající. Nás nezajímá jedna konkrétní situace, chtěli bychom se na model podívat globálně.

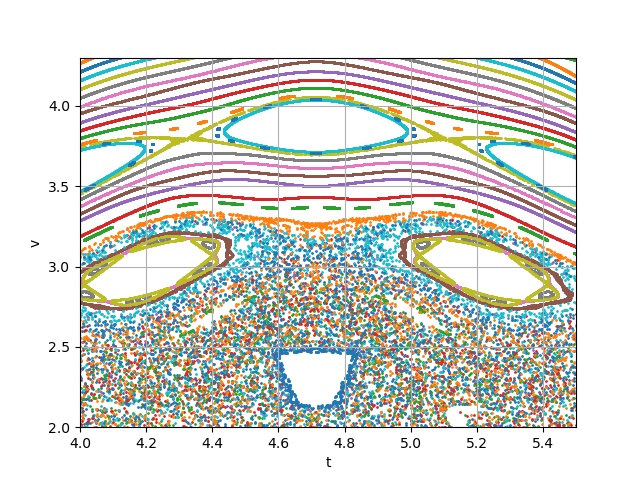
Stav kuličky, resp. systému "kulička-zdi", je popsán časem, rychlostí kuličky a polohou kuličky. Idealizovaně jde o bod v trojrozměrném prostoru (tzv. fázovém prostoru). Časový vývoj systému v tomto prostoru vytváří křivku (trajektorii).

Abychom vývoj ve fázovém prostoru mohli přehledně znázornit, využijeme k tomu techniku Poincarého řezů: v našem trojrozměrném prostoru zvolíme plochu, kterou trajektorie procházejí, a zaznamenáme tyto body průchodu. Body příslušející stejné trajektorii můžeme třeba obarvit stejnou barvou.

V našem případě je situace poměrně jednoduchá. Budeme zaznamenávat čas a rychlost kuličky při odrazu na pevné zdi (tj. když prochází rovinou $x=0$ ). Navíc stačí zaznamenávat čas modulo perioda oscilace zdi (pokud bychom se v čase posunuli o násobek této periody, tak se systém bude vyvíjet stejně - pohyblivá zeď v těchto okamžicích je ve stejné konfigurace, pro kuličku to jsou nerozlišitelné situace). Pro ilustraci viz ukázkový obrázek níže.

Implementační pokyny

V souboru fermi-ulam.jl vytvořte modul FermiUlam, který bude exportovat následující metody a typy:

Typ `Wall`

Julia typ zachycující vlastnosti pohyblivé zdi, které popíšeme následujícími atributy.

position: závislost polohy zdi na čase.
dposition: derivace závislosti polohy zdi na čase (tj. rychlost zdi v daném časovém okamžiku).
bounds: vektor o dvou složkách obsahující dolní a horní hranici oboru hodnot zdi (tj. interval, kde se zeď může pohybovat).
period: perioda oscilace.

Zajistěte, aby při konstrukci zdi bylo zkontrolováno, že:

bounds je dvousložkový vektor, horní hranice je větší nebo rovna spodní hranici,
hodnota period nemůže být záporná,
dolní mez bounds musí být kladná (tj. pohyblivá zeď je vpravo od bodu $0$ ).

V souboru fermi-ulam.jl je dále předpřipraven pomocný konstruktor StaticWall vytvářející nepohyblivou zeď v daném bodě. Ten se hodí zejména při testování.

Metoda `evolution`

Toto je hlavní metoda tohoto úkolu. Pro zadanou pohyblivou zeď wall a počáteční rychlost kuličky v startující v čase t (nepovinný parametr, výchozí hodnota 0) vypočte nhits zpětných odrazů a zaznamená čas a rychlost kuličky při odrazu na pevné zdi. Čas počítáme modulo perioda (z pohledu časového vývoje posun času o periodu nehraje roli, systém se bude vyvíjet stejně).

Metoda vrací pole data (možno předat předpřipraveno pomocí keyword argumentu), které má nhits+1 řádků s 2 sloupce. V prvním sloupci je čas (modulo perioda) a v druhém rychlost při odrazu na nepohyblivé zdi (včetně počátečních hodnot).

Metoda `inspect`

Tato metoda se snaží vizualizovat část fázového prostoru. Jde o více kreativní a experimentální partii úkolu a proto není nijak extra svázána požadavky. Jediné omezení, které na ni klademe je přijímání následujících tří pozičních argumentů:

wall: použitá zeď,
tbounds: časový rozsah výřezu, tj. [t1, t2],
vbounds: rychlostní rozsah výřezu, tj. [v1, v2].

Jaký použijete grafický balíček, nebo jaké si přidáte pomocné keyword argumenty kontrolující parametry výpočtu je na vás.

Ukázkové použití této metody najdete v souboru fermi-ulam.ipynb, který můžete také modifikovat a odevzdat. Zkuste fázový prostor prozkoumat, najděte zajímavé oblasti! Z nejhezčích obrázků udělám galerii.

HINT: Jako nejvhodnější typ grafu se zde nabízí scatter plot, šlo by i uvažovat o čistém matrix plot, aby se dosáhlo plného pokrytí fázového prostoru. Obarvení může být také důležité a kreativitě meze neklademe. Pro inspiraci viz fermi-ulam.ipynb.

Řez fázového prostoru. — Obrázek 3. Ŕez fázového prostoru.

Neexportovaná metoda `root`

Tato metoda hledá nulový bod funkce func, její signatura je následující

root(func::Function, xs::Vector{Float64}; max_iter=10_000, atol=sqrt(eps(Float64)))

Pokud používáte metodu sečny, pak xs je vektor obsahující dvě aproximace nulového bodu. Nepovinné argumenty představují maximální počet iterací max_iter a absolutní toleranci atol, která kontroluje zastavení výpočtu.

Pokud nepoužijete metodu sečny, můžete tuto funkci i její signaturu vhodně modifikovat, ale budete pak muset vhodně modifikovat i příslušné testy.

Lokální spouštění testů

K lokálnímu spuštění testů budete pravděpodobně potřebovat doinstalovat balíček Glob.

import Pkg; Pkg.add("Glob")

Poté v kořenovém adresáři tohoto zadání stačí z příkazové řádky spustit

$ julia --color=yes test/runtests.jl

Tímto příkazem spustíte všechny test v souborech test/test_*.jl. Případně tak do adresáře test můžete snadno přidat i další pomocné vlastní testy vlastních pomocných metod, jen je musíte pojmenovat ve tvaru test_*.jl.

Pokud vše dopadne dobře, měli byste vidět následující standardní výstup:

$ julia test/runtests.jl
┌ Info: Running tests in test_evolution.jl...
└ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Test Summary:                                                | Pass  Total
exceptions in the evolution method                           |    2      2
Test Summary:                                                | Pass  Total
evolution in different regimes                               |    4      4
Test Summary:                                                | Pass  Total
staged evolution                                             |    3      3
┌ Info: Running tests in test_other.jl...
└ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
┌ Info: Running tests in test_root.jl...
└ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Test Summary:                                                | Pass  Total
root finding: linear                                         |    1      1
Test Summary:                                                | Pass  Total
root finding: quadratic                                      |    2      2
Test Summary:                                                | Pass  Total
root finding: cubic                                          |    1      1
Test Summary:                                                | Pass  Total
root finding: trigonometric                                  |    1      1
Test Summary:                                                | Pass  Total
root finding: logarithm                                      |    1      1
Test Summary:                                                | Pass  Total
root finding: non-smooth                                     |    2      2
Test Summary:                                                | Pass  Total
root finding: exceptions                                     |    1      1
┌ Info: Running tests in test_static_wall.jl...
└ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Test Summary:                                                | Pass  Total
static wall                                                  |    3      3
Test Summary:                                                | Pass  Total
accelerating wall                                            |    1      1
Test Summary:                                                | Pass  Total
decelerating wall                                            |    1      1
┌ Info: Running tests in test_wall.jl...
└ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Test Summary:                                                | Pass  Total
exceptions in the wall constructor                           |    4      4

V opačném případě dostanete od Julia vynadáno!

Varování:

Pokud budete pro práci s grafikou používat jiný balíček, než je PyPlot, nebo budete potřebovat další balíček doinstalovat, pak musíte upravit sedmý řádek souboru gitlab-ci.yml. Tj. přidat váš balíček, aby byl k dispozici i v testovacím prostředí na gitlabu.

Řešení a odevzdání

Opět vytvořte větev odvozenou z větve assignment/02-fermi-ulam a nezvěte ji například solution/02-fermi-ulam. Do solution/02-fermi-ulam vložte své řešení editací souboru fermi-ulam.jl případně přidáním testů do složky test a ideálně modifikujte i fermi-ulam.ipynb a doplňte ho o vlastní pokusy. Až budete se svým řešením spokojeni, vytvořte MR (to můžete i dříve, aspoň uvidíte výsledek testů, pokud je nespouštíte lokálně) a přiřaďte mě k němu jako assignee. Tímto aktem úkol odevzdáte.

Poznámky

Odkazy na literaturu

[1] E. Fermi, On the Origin of the Cosmic Radiation, Phys. Rev. 75 (8), 1949, 1169-1174.
[2] S. Ulam, On the Statistical Properties of Dynamical Systems, Proc. 4th Berkeley Symp. Math. Stat. Probab. 3, 1961, 315-320.